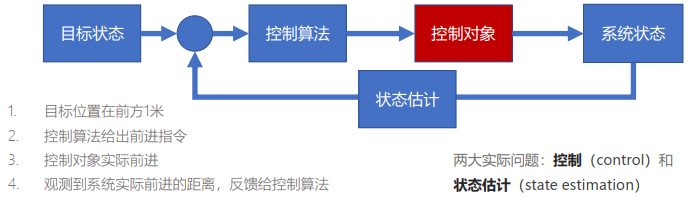
【状态估计】概率基础
引言
- 传感器可分为两大类
- 内感受型(interoceptive):测量运动主体的速度、加速度等信息
- 外感受型(exteroceptive):测量运动主体的位置、朝向等信息
- 内感受型传感器
- 加速度计:测量平移加速度
- 陀螺仪:测量角速度
- 惯性测量单元IMU:三轴线性加速度计和三轴陀螺仪
- 轮式编码器:测量转动频率
- 外感受型传感器
- 相机、激光、毫米波
- GPS
- 最好的状态估计同时有效利用内感受型和外感受型传感器的观测值
- 状态估计:根据系统的先验模型和测量序列,对系统内在状态进行重构的问题
概率基础:概率密度函数
基本定义
概率与概率密度
- 定义x为区间[a,b]上的随机变量(random variable),服从某个概率密度函数p(x),则有:
- 非负性:\forall x\in[a,b],p(x)\ge 0
- 归一性:\int_a^b p(x) \mathrm{d}x=1
- 概率密度和概率的区别
- 概率密度函数(probability density functions, PDFs)
- 概率(probability)是指PDF在某区间上的积分面积
- x落在区间[c,d]的概率为\mathrm{Pr}(c\le x\le d)=\int_c^d p(x) \mathrm{d}x
- 当x表示某种状态时,也称为x在该区间下的可能性/似然(likehood)
条件、联合、边缘概率
- 条件概率密度:p(x | y)表示自变量x\in[a,b]在条件y\in[r,s]下的概率密度函数
- (\forall y)\quad \int_a^b p(x | y)\mathrm{d}x=1
- 联合概率密度:p(x_1,x_2,\cdots,x_N)
- 满足全概率公理
- \int_a^bp(x)\mathrm{d}x=\int_{a_N}^{b_N}\cdots\int_{a_2}^{b_2}\int_{a_1}^{b_1}p(x_1,x_2,\cdots,x_N)\mathrm{d}x_1\mathrm{d}x_2\cdots\mathrm{d}x_N=1
- 边缘概率密度:p(x,y)=p(x|y)p(y)=p(y|x)p(x)
- 联合=条件\times边缘
- x和y独立时:p(x,y)=p(x)p(y)
贝叶斯估计
贝叶斯公式
p(x | y)=\frac{p(y|x)p(x)}{p(y)}
- 贝叶斯公式(Bayes’ Rule):
- 先验(prior):p(x)
- 观测数据:y
- 似然(传感器模型):p(y|x)
- 后验(posterior):p(x|y)
- 分母可通过边缘化(marginalization)求解
\begin{gathered} p(y) =p(y)\underbrace{\int p(x|y)\mathrm{d}x}_{1}=\int p(x|y)p(y)\mathrm{d}x \\ =\int p(x,y)\mathrm{d}x=\int p(y|x)p(x)\mathrm{d}x \end{gathered}
矩估计
- 矩(moments)在统计上描述概率密度的形状
- 概率的零阶矩:整个全事件的概率,恒定为1
- 概率的一阶矩:期望(Expectation),表示随机变量平均取值的大小
- \mu=E\left[x\right]=\int xp\left(x\right)\mathrm{d}x
- E[\cdot]表示期望算子,矩阵函数F(x)的期望E[F(x)]=\int F(x)p(x)\mathrm{d}x
- 概率的二阶矩:协方差(Covariance),衡量两个变量的总体误差
- \Sigma=E\left[(x-\mu)(x-\mu)^{\mathrm{T}}\right]
- \mathrm{Cov}(X,Y)=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]
- 概率的三阶矩为偏度(Skewness),四阶矩为峰度(Kurtosis)
统计基础
样本均值和方差
- 若只使用一阶矩和二阶矩刻画某个分布,则等同于近似为高斯分布
- 样本(measurement) :随机变量的一次实现(realization)
- 随机变量x的PDF为p(x),则从密度函数抽样x_{meas}\leftarrow p(x)
- 传感器测量数据可视为一个变量的样本
- 通过多个样本计算随机变量的一阶矩和二阶矩
\begin{aligned} &\mu_{\mathrm{meas}} =\frac1N\sum_{i=1}^Nx_{i,\text{meas}} \\ &\Sigma_{\mathrm{meas}} =\frac1{N-1}\sum_{i=1}^N(x_{i,\text{meas}} - \mu _ {\text{meas}} ) ( x _ { i ,\text{meas}} - \mu _ {\text{meas}} ) ^ \mathrm{T} \end{aligned}
- 贝塞尔修正(Bessel’s correction):二阶矩的归一化分母为N-1
- 样本方差由测量值和样本均值的差得到,样本均值是通过相同测量值得到的
- N个样本的样本方差自由度为N-1,一个自由度由于均值被消去
- 样本方差是随机变量的无偏估计,通过贝塞尔修正将原本的有偏估计修正为无偏估计
统计独立与不相关性
- 统计独立(Statistically Independent):
- 两个随机变量x和y的联合PDF满足p(x,y)=p(x)p(y)
- 不相关的(Uncorrelated):
- 两个随机变量x和y的期望运算满足
- E[xy^\mathrm{T}]=E[x]E[y]^\mathrm{T}
- 独立性可推导出不相关性,反之不行;对于高斯分布而言两者相等
计算与信息论
归一化积(重点)
-
归一化积(Normalized Product):计算同一个随机变量的两个不同概率密度函数
- p(x)=\eta p_1(x)p_2(x)
- \eta为归一化因子,通常是一个数,保证全概率公理
- \eta=\Big(\int p_1(x) p_2(x) \mathrm{d}x\Big)^{-1}
-
使用归一化积融合对同一个随机变量的多次估计
-
x是一个代估计状态(随机变量),y_1和y_2为两次独立的观测
-
p(x|y_1,y_2)=\eta p(x|y_1)p(x|y_2)
-
使用贝叶斯公式推导归一化积
-
\begin{align} p(x|y_1,y_2)=&\frac{p(y_1,y_2|x)p(x)}{p(y_1,y_2)}\\ p(y_1,y_2|x)=&p(y_1|x)p(y_2|x)\\ =&\frac{p(x|y_1)p(y_1)}{p(x)}\frac{p(x|y_2)p(y_2)}{p(x)}\\ p(x|y_1,y_2)=&\eta p(x|y_1)p(x|y_2)\\ \eta=&\frac{p(y_1)p(y_2)}{p(y_1,y_2)p(x)}=\frac{1}{p(x)} \end{align}
- 若先验p(x)为均匀分布(即取常数),则\eta也是一个常量
香农信息和互信息
-
香农信息(Shannon Information):刻画某个随机变量的不确定性
- 又称为负熵(Negative Entropy),描述分布的混乱程度
- H(x)=-E[\ln p(x)]=-\int p(x)\ln p(x)\mathrm{d}x
-
互信息(Mutual Information):两个随机变量x和y之间的不确定性
- 刻画已知一个随机变量的信息后,另一个随机变量的不确定性减少多少
- 两个随机变量相互独立时,互信息为0
- 不独立时I(x,y)\ge 0,满足下式第三行
\begin{align} I(x,y)=&E\left[\ln\left(\frac{p(x,y)}{p(x)p(y)}\right)\right]\\ =&\iint p(x,y)\ln\left(\frac{p(x,y)}{p(x)p(y)}\right)\mathrm{d}x\mathrm{d}y\\ =&H(x)+H(y)-H(x,y) \end{align}
高斯概率
基本定义
一维高斯Gauss
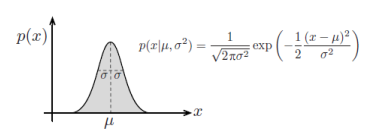
- p(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right)
- \mu为均值(mean)、\sigma^2为方差(variance)、\sigma为标准差(standard deviation)
- 高斯分布的期望和模(mode,众数,最可能的取值)均为\mu
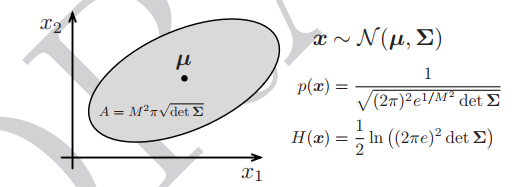
多维高斯
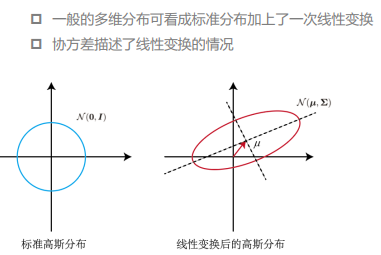
- p(x|\mu,\Sigma)=\frac{1}{\sqrt{(2\pi)^N\det\Sigma}}\exp\left(-\frac{1}{2}(x-\mu)^{\text{T}}\Sigma^{-1}(x-\mu)\right)
- \mu为均值、\Sigma\in \R^{N\times N}为协方差矩阵(对称正定矩阵)
\begin{aligned} \mu&=E[x] \\ &=\int_{-\infty}^{\infty}x\frac{1}{\sqrt{(2\pi)^N\det\Sigma}}\exp\left(-\frac{1}{2}(x-\mu)^{\text{T}}\Sigma^{-1}(x-\mu)\right)\mathrm{d}x \\ \Sigma& =E\left[(x-\mu)(x-\mu)^{\mathrm{T}}\right] \\ &=\int_{-\infty}^{\infty}(x-\mu)(x-\mu)^{\mathrm{T}}\frac{1}{\sqrt{(2\pi)^{N}\det\Sigma}}\exp\left(-\frac{1}{2}(x-\mu)^{\mathrm{T}}\Sigma^{-1}(x-\mu)\right)\mathrm{d}x \end{aligned}
高斯推断与独立性
矩阵理论:舒尔补
-
舒尔补Schur Complement
-
分块矩阵\begin{pmatrix}A&B\\C&D\end{pmatrix}中A和D均为方块
-
D的舒尔补为\widetilde{D}=D-CA^{-1}B
-
A的舒尔补为\widetilde{A}=A-BD^{-1}C
-
联合高斯
- 一对服从多元正态分布的变量(x,y),其联合高斯概率密度函数为:
- \left.\left.p(x,y)=\mathcal{N}\left(\left[\begin{array}{c}\mu_x\\\mu_y\end{array}\right.\right.\right],\left[\begin{array}{cc}\Sigma_{xx}&\Sigma_{xy}\\\Sigma_{yx}&\Sigma_{yy}\end{array}\right]\right)
- 协方差矩阵对称正定,则\Sigma_{yx}=\Sigma_{xy}^\mathrm{T}
- 联合高斯可分解为条件概率乘以边缘概率:p(x,y)=p(x| y)p(y)
高斯推断
- 使用Schur补将联合高斯分布的协方差矩阵对角化,再两侧取逆
\begin{align} \left.\left[\begin{array}{cc}\Sigma_{xx}&\Sigma_{xy}\\\Sigma_{yx}&\Sigma_{yy}\end{array}\right.\right]=&\left[\begin{array}{cc}1&\Sigma_{xy}\Sigma_{yy}^{-1}\\0&1\end{array}\right]\left[\begin{array}{cc}\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}&0\\0&\Sigma_{yy}\end{array}\right]\left[\begin{array}{cc}1&0\\\Sigma_{yy}^{-1}\Sigma_{yx}&1\end{array}\right]\\ \left.\left[\begin{array}{cc}\Sigma_{xx}&\Sigma_{xy}\\\Sigma_{yx}&\Sigma_{yy}\end{array}\right.\right]^{-1}=&\left[\begin{array}{cc}1&0\\-\Sigma_{yy}^{-1}\Sigma_{yx}&1\end{array}\right]\left[\begin{array}{cc}\left(\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right)^{-1}&0\\0&\Sigma_{yy}^{-1}\end{array}\right]\left[\begin{array}{cc}1&-\Sigma_{xy}\Sigma_{yy}^{-1}\\0&1\end{array}\right] \end{align}
- 考虑p(x,y)的指数部分内容,将上述对角化求逆结果带入
$$
\begin{aligned}
&\left(\left[\begin{array}{c}x\y\end{array}\right]
-\left[\begin{array}{c}\mu_x\\mu_y\end{array}\right]\right)^{\mathrm{T}}
\left[\begin{array}{cc}\Sigma_{xx}&\Sigma_{xy}\\Sigma_{yx}&\Sigma_{yy}\end{array}\right]^{-1}
\left(\left[\begin{array}{c}x\y\end{array}\right]-\left[\begin{array}{c}\mu_x\\mu_y\end{array}\right]\right) \
&=\left[\begin{array}{c}x-\mu_x\y-\mu_y\end{array}\right]^{\mathrm{T}}
\left[\begin{array}{cc}1&0\-\Sigma_{yy}^{-1}\Sigma_{yx}&1\end{array}\right]
\left[\begin{array}{cc}\left(\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}{-1}\Sigma_{yx}\right){-1}&0\0&\Sigma_{yy}^{-1}\end{array}\right]
\left[\begin{array}{cc}1&-\Sigma_{xy}\Sigma_{yy}^{-1}\0&1\end{array}\right]
\left[\begin{array}{c}x-\mu_x\y-\mu_y\end{array}\right] \
=& \left[\begin{matrix}{x-\mu_{x}-\sum_{xy}\Sigma_{yy}{-1}\left(y-\mu_{y}\right)}\{y-\mu_{y}}\\end{matrix}\right]{\mathrm{T}}
\left[\begin{matrix}{\left(\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}{-1}\Sigma_{yx}\right){-1}}&{0}\{0}&{\Sigma_{yy}^{-1}}\end{matrix}\right]
\left[\begin{matrix}{x-\mu_{x}-\Sigma_{xy}\Sigma_{yy}^{-1}\left(y-\mu_{y}\right)}\{y-\mu_{y}}\end{matrix}\right]\
=&\left(x-\mu_x-\Sigma_{xy}\Sigma_{yy}{-1}\left(y-\mu_y\right)\right){\mathrm{T}}
\left(\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}{-1}\Sigma_{yx}\right){-1} \left(x-\mu_{x}-\Sigma_{xy}\Sigma_{yy}^{-1}\left(y-\mu_{y}\right)\right)
+\left(y-\mu_{y}\right){\mathrm{T}}\Sigma_{yy}{-1}\left(y-\mu_{y}\right)
\end{aligned}
$$
- 上述结果为联合高斯在指数上的两个二项式的加和,则指数上的加法等同于底数上的乘法
- 联合:p(x,y)=p(x|y)p(y)
- 条件:p(x|y)=\mathcal{N}\left(\mu_{x}+\Sigma_{xy}\Sigma_{yy}^{-1}\left(y-\mu_{y}\right),\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right)
- 边缘:p(y)=\mathcal{N}\left(\mu_y,\Sigma_{yy}\right)
- 整个过程称为高斯推断(Gaussian Inference)
- 应用中通常已知联合和边缘,要求条件概率
- 条件概率的协方差降低,说明不确定性降低
统计独立与不相关性
- 高斯分布的独立性和不相关性等价
- 若x和y不相关,则\Sigma_{xy}=0
- p(x|y)=\mathcal{N}\left(\mu_{x}+\Sigma_{xy}\Sigma_{yy}^{-1}\left(y-\mu_{y}\right),\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right)=\mathcal{N}\left(\mu_{x},\Sigma_{xx}\right)=p(x)
- 则x和y相互独立
- 不相关性条件:E[xy^T]=E[x]E[y]^T
变换计算
高斯线性变换
- 已知随机变量\begin{aligned}x\in\mathbb{R}^N\sim\mathcal{N}(\mu_x,\Sigma_{xx})\end{aligned},现研究另一随机变量y=Gx的统计特性
- G\in\R^{M\times N}为常量矩阵,可直接计算y的均值、方差
\begin{aligned} \mu_{y}=&E[y]=E\left[Gx\right]=GE\left[x\right]=G\mu_{x} \\ \Sigma_{yy}=&E\left[\left(y-\mu_{y}\right)\left(y-\mu_{y}\right)^{\mathrm{T}}\right] \\ =&GE\left[\left(x-\mu_{x}\right)\left(x-\mu_{x}\right)^{\mathrm{T}}\right]G^{\mathrm{T}}\\ =&G\Sigma_{xx}G^{\mathrm{T}} \end{aligned}
高斯归一化积(重点)
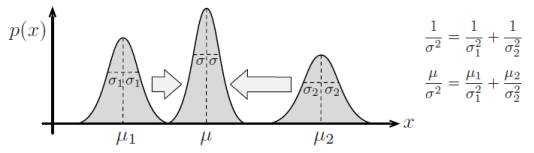
- K个不同高斯分布的归一化积仍然是一个高斯分布
\begin{align} \exp\left(-\frac{1}{2}\left(x-\mu\right)^{\mathrm{T}}\Sigma^{-1}\left(x-\mu\right)\right)\equiv\eta\prod_{k=1}^{K}\exp&\left(-\frac{1}{2}\left(x-\mu_{k}\right)^{\mathrm{T}}\Sigma_{k}^{-1}\left(x-\mu_{k}\right)\right)\\ \Sigma^{-1}=\sum_{k=1}^{K}\Sigma_{k}^{-1}\\ \Sigma^{-1}\mu=\sum_{k=1}^{K}\Sigma_{k}^{-1}\mu_{k} \end{align}
- 高斯分布随机变量的线性变换如下:G_k\in\R^{M_k\times N}\ (M_k\le N)
\begin{align} \exp\left(-\frac{1}{2}\left(x-\mu\right)^{\mathrm{T}}\Sigma^{-1}\left(x-\mu\right)\right)\equiv\eta\prod_{k=1}^{K}\exp&\left(-\frac{1}{2}\left(G_kx-\mu_{k}\right)^{\mathrm{T}}\Sigma_{k}^{-1}\left(G_kx-\mu_{k}\right)\right)\\ \Sigma^{-1}=\sum_{k=1}^{K}G_k^\mathrm{T}\Sigma_{k}^{-1}G_k\\ \Sigma^{-1}\mu=\sum_{k=1}^{K}G_k^\mathrm{T}\Sigma_{k}^{-1}\mu_{k} \end{align}
矩阵求逆引理:SMW恒等变换
- 可逆矩阵可通过三角分解变换得到LDU和UDL形式
\begin{align} &\quad\ \left[\begin{array}{rr}A^{-1}&-B\\C&D\end{array}\right] \\ &=\left[\begin{array}{cc}1&0\\CA&1\end{array}\right]\left[\begin{array}{cc}A^{-1}&0\\0&D+CAB\end{array}\right]\left[\begin{array}{cc}1&-AB\\0&1\end{array}\right]\qquad\mathrm{(LDU)} \\ &=\left[\begin{array}{cc}1&-BD^{-1}\\0&1\end{array}\right]\left[\begin{array}{cc}A^{-1}+BD^{-1}C&0\\0&D\end{array}\right]\left[\begin{array}{cc}1&0\\D^{-1}C&1\end{array}\right]\qquad\mathrm{(UDL)} \end{align}
- 分别对LDU和UDL求逆,对应分块部分相等得到SMW恒等式
- 下三角矩阵的逆L^{-1}=\frac{adj(L)}{det L}=adj(L)
- 上三角矩阵的逆U^{-1}=\frac{adj(U)}{det U}=adj(U)
- 对角矩阵的逆D^{-1}为对角线上元素各自求逆
$$
\begin{align}
&\quad\ \left[\begin{array}{rr}A{-1}&-B\C&D\end{array}\right]{-1} \
&=\left[\begin{array}{cc}1&-AB\0&1\end{array}\right] \left[\begin{array}{cc}A&0\0&(D+CAB)^{-1}\end{array}\right] \left[\begin{array}{cc}1&0\-CA&1\end{array}\right] \
&=\left[\begin{array}{cc}A-AB\left(D+CAB\right){-1}CA&AB\left(D+CAB\right){-1}\-\left(D+CAB\right){-1}CA&\left(D+CAB\right){-1}\end{array}\right] \\
&\quad\ \left[\begin{array}{rr}A{-1}&-B\C&D\end{array}\right]{-1} \
&=\left[\begin{array}{cc}1&0\-D^{-1}C&1\end{array}\right] \left[\begin{array}{cc}A{-1}+BD{-1}C&0\0&D\end{array}\right] \left[\begin{array}{cc}1&BD^{-1}\0&1\end{array}\right] \
&=\left[\begin{array}{cc}\left(A{-1}+BD{-1}C\right){-1}&\left(A{-1}+BD{-1}C\right){-1}BD{-1}\-D{-1}C\left(A{-1}+BD{-1}C\right){-1}&D{-1}-D{-1}C\left(A{-1}+BD{-1}C\right){-1}BD^{-1}\end{array}\right]
\end{align}
$$
- 对应相等,得到SMW恒等式,再处理高斯PDF的协方差矩阵时常被用到
\begin{aligned} \left(A^{-1}+BD^{-1}C\right)^{-1}& \equiv A-AB\left(D+CAB\right)^{-1}CA \\ \left(D+CAB\right)^{-1}& \equiv D^{-1}-D^{-1}C\left(A^{-1}+BD^{-1}C\right)^{-1}BD^{-1} \\ AB\left(D+CAB\right)^{-1}& \equiv\left(A^{-1}+BD^{-1}C\right)^{-1}BD^{-1} \\ \left(D+CAB\right)^{-1}CA& \equiv D^{-1}C\left(A^{-1}+BD^{-1}C\right)^{-1} \end{aligned}
高斯非线性变换
- 非线性映射
- 随机变量x\in\R\sim\mathcal{N}(\mu_x,\Sigma_{xx}),非线性映射g:x\to y
- p\left(y|x\right)=\mathcal{N}\left(g\left(x\right),R\right),噪声为R
- 线性化处理:再某点(x均值)处线性化,近似为线性变换
- G为该点雅可比
- 线性化可看作为一阶泰勒展开
\begin{aligned} \boldsymbol{g}\left(\boldsymbol{x}\right)& \approx\mu_y+G\left(x-\mu_x\right) \\ \text{G}& =\left.\frac{\partial\boldsymbol{g}(x)}{\partial x}\right|_{\boldsymbol{x}=\boldsymbol{\mu}_x} \\ \mu_{y}& =g\left(\mu_{x}\right) \end{aligned}
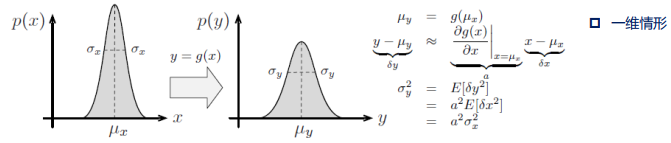
- 高维情况下由贝叶斯公式进一步化简:
- 将积分项分为三部分相乘:无关项(y-\mu_y)、相关项(x-\mu_x)、混合项
- 无关项与x无关,移出积分
\begin{aligned} p(\boldsymbol{y})& =\int_{-\infty}^{\infty}p\left(y|x\right)p(x)\mathrm{d}x \\ &=\eta\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}\left(y-\left(\mu_{y}+G\left(x-\mu_{x}\right)\right)\right)^{\mathrm{T}}R^{-1}\left(y-\left(\mu_{y}+G\left(x-\mu_{x}\right)\right)\right)\right) \\ &\times\exp\left(-\frac{1}{2}\left(x-\mu_{x}\right)^{\mathrm{T}}\Sigma_{xx}^{-1}\left(x-\mu_{x}\right)\right)\mathrm{d}x \\ &=\eta\color{red}\boxed{\exp\left(-\frac{1}{2}\left(y-\mu_{y}\right)^{\mathrm{T}}R^{-1}\left(y-\mu_{y}\right)\right)} \\ &\times\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}\left(x-\mu_{x}\right)^{\mathrm{T}}\left(\Sigma_{xx}^{-1}+G^{\mathrm{T}}R^{-1}G\right)(x-\mu_{x})\right) \\ &\times\exp\left(\left(y-\mu_{y}\right)^{\mathrm{T}}R^{-1}G\left(x-\mu_{x}\right)\right)\mathrm{d}x \end{aligned}
- 配方法进一步化简
- 为凑平方交叉项系数,定义F^{\mathrm{T}}\left(G^{\mathrm{T}}R^{-1}G+\Sigma_{xx}^{-1}\right)=R^{-1}G
- 构造类似a^2-2ab=(a-b)^2-b^2
- 第二项与x无关,移除积分
- 第一项积分后为常数,归于归一化因子
\begin{aligned}&\exp\left(-\frac{1}{2}\left(x-\mu_x\right)^{\mathrm{T}}\left(\Sigma_{xx}^{-1}+G^{\mathrm{T}}R^{-1}G\right)\left(x-\mu_x\right)\right)\times\exp\left(\left(y-\mu_y\right)^{\mathrm{T}}R^{-1}G\left(x-\mu_x\right)\right)\\=&\exp\left(-\frac{1}{2}\left(\left(x-\mu_x\right)-F\left(y-\mu_y\right)\right)^{\mathrm{T}}\left(G^{\mathrm{T}}R^{-1}G+\Sigma_{xx}^{-1}\right)\left(\left(x-\mu_x\right)-F\left(y-\mu_y\right)\right)\right)\\ &\color{red}\boxed{\times\exp\left(\frac{1}{2}\left(y-\mu_y\right)^{\mathrm{T}}F^{\mathrm{T}}\left(G^{\mathrm{T}}R^{-1}G+\Sigma_{xx}^{-1}\right)F\left(y-\mu_y\right)\right)}\end{aligned}
- 提取出积分的部分构成先验
\begin{aligned} p(y)& =\rho\exp\left(-\frac{1}{2}\left(y-\mu_{y}\right)^{\mathrm{T}}\left(R^{-1}-F^{\mathrm{T}}\left(G^{\mathrm{T}}R^{-1}G+\Sigma_{xx}^{-1}\right)F\right)\left(y-\mu_{y}\right)\right) \\ &=\rho\exp\left(-\frac{1}{2}\left(y-\mu_{y}\right)^{\mathrm{T}}\left(\underbrace{R^{-1}-R^{-1}G\left(G^{\mathrm{T}}R^{-1}G+\Sigma_{xx}^{-1}\right)^{-1}G^{\mathrm{T}}R^{-1}}_{\color{red}{\mathrm{SMW(a)}}}\right)(y-\mu_{y})\right) \\ &=\rho\exp\left(-\frac{1}{2}\left(y-\mu_{y}\right)^{\mathrm{T}}\left(R+G\Sigma_{xx}G^{\mathrm{T}}\right)^{-1}\left(y-\mu_{y}\right)\right) \end{aligned}
- 得到y的高斯分布为:y\sim\mathcal{N}\left(\mu_{y},\Sigma_{yy}\right)=\mathcal{N}\left(g\left(\mu_{x}\right),R+G\Sigma_{xx}G^{\mathrm{T}}\right)
信息论
高斯香农信息
- 由香浓信息熵定义带入高斯分布定义式
- 高斯分布的无穷积分为1
- 第二项为平方马氏距离的期望值
\begin{aligned} H\left(x\right)& =-\int_{-\infty}^{\infty}p\left(\boldsymbol{x}\right)\ln p\left(\boldsymbol{x}\right)d\boldsymbol{x} \\ &=-\int_{-\infty}^{\infty}p\left(\boldsymbol{x}\right)\left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)-\ln\sqrt{\left(2\pi\right)^{N}\det\boldsymbol{\Sigma}}\right)\mathrm{d}\boldsymbol{x} \\ &={\color{red}\boxed{\ln\left(\left(2\pi\right)^{N}\det\boldsymbol{\Sigma}\right)^{\frac{1}{2}}\int_{-\infty}^{+\infty}\boldsymbol{p}(\boldsymbol{x})\mathrm{d}x}}+\int_{-\infty}^{\infty}\frac{1}{2}\left(x-\boldsymbol{\mu}\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\boldsymbol{p}\left(\boldsymbol{x}\right)\mathrm{d}x \\ &=\frac{1}{2}\ln\left(\left(2\pi\right)^{N}\det\boldsymbol{\Sigma}\right)+\int_{-\infty}^{\infty}\frac{1}{2}\left(x-\boldsymbol{\mu}\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\boldsymbol{p}\left(\boldsymbol{x}\right)\mathrm{d}x \\ &=\frac{1}{2}\ln\left(\left(2\pi\right)^{N}\det\boldsymbol{\Sigma}\right)+\frac{1}{2}E\left[\left(x-\boldsymbol{\mu}\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\right] \end{aligned}
- 马氏距离
- 与欧氏距离类似,但考虑协方差矩阵的逆做加权
- 二次型可用迹(trace)重写
- \left(x-\mu\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(x-\mu\right)=\mathrm{tr}\left(\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^{\mathrm{T}}\right)
\begin{aligned} E\left[\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^{\mathrm{T}}\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\right]& =\mathrm{tr}\left(E\left[\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^{\mathrm{T}}\right]\right) \\ &=\operatorname{tr}\left(\boldsymbol{\Sigma}^{-1}\underbrace{E\left[\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^{\mathrm{T}}\right]}_{\boldsymbol{\Sigma}}\right) \\ &=\mathrm{tr}\left(\Sigma^{-1}\Sigma\right) \\ &=tr1 \\ &=N \end{aligned}
- 带回原式,进一步化简得到如下表达:
- \sqrt{\mathrm{det}\Sigma}为高斯概率密度函数构成的不确定性椭球体积
\begin{aligned} H\left(x\right)& =\frac{1}{2}\ln\left(\left(2\pi\right)^{N}\det\Sigma\right)+\frac{1}{2}E\left[\left(x-\mu\right)^{T}\Sigma^{-1}\left(x-\mu\right)\right] \\ &=\frac{1}{2}\ln\left(\left(2\pi\right)^{N}\det\Sigma\right)+\frac{1}{2}N \\ &=\frac{1}{2}\left(\ln\left(\left(2\pi\right)^{N}\det\Sigma\right)+N\ln e\right) \\ &=\frac{1}{2}\ln\left(\left(2\pi e\right)^{N}\det\Sigma\right) \end{aligned}
高斯互信息
- 随机变量x\in\R^N和y\in\R^N,其联合高斯分布为:\left.\left.p\left(\boldsymbol{x},\boldsymbol{y}\right)=\mathcal{N}\left(\boldsymbol{\mu},\boldsymbol{\Sigma}\right)=\mathcal{N}\left(\left[\begin{array}{c}\boldsymbol{\mu}_{x}\\\boldsymbol{\mu}_{y}\end{array}\right.\right.\right],\left[\begin{array}{cc}\boldsymbol{\Sigma}_{xx}&\boldsymbol{\Sigma}_{xy}\\\boldsymbol{\Sigma}_{yx}&\boldsymbol{\Sigma}_{yy}\end{array}\right]\right)
- 若两随机变量不独立,则由I(x,y)=H(x)+H(y)-H(x,y)进一步推导:
\begin{aligned} I\left(\boldsymbol{x},\boldsymbol{y}\right)& =\frac{1}{2}\ln\big((2\pi e)^N\det\boldsymbol{\Sigma}_{xx}\big)+\frac{1}{2}\ln\big((2\pi e)^M\det\boldsymbol{\Sigma}_{yy}\big) \\ &-\frac{1}{2}\ln\big((2\pi e)^{M+N}\det\boldsymbol{\Sigma}\big) \\ &=-\frac12\ln\left(\frac{\det\boldsymbol{\Sigma}}{\det\boldsymbol{\Sigma}_{xx}\det\boldsymbol{\Sigma}_{yy}}\right) \end{aligned}
- 高斯推断中使用舒尔补得到的\Sigma矩阵分解形式可知:
- \det\boldsymbol{\Sigma}=\det\boldsymbol{\Sigma}_{xx}\det\left(\boldsymbol{\Sigma}_{yy}-\boldsymbol{\Sigma}_{yx}\boldsymbol{\Sigma}_{xx}^{-1}\boldsymbol{\Sigma}_{xy}\right)
- \det\boldsymbol{\Sigma}=\det\boldsymbol{\Sigma}_{yy}\det\left(\boldsymbol{\Sigma}_{xx}-\boldsymbol{\Sigma}_{xy}\boldsymbol{\Sigma}_{yy}^{-1}\boldsymbol{\Sigma}_{yx}\right)
- 带入上述,可知高斯互信息:
\begin{aligned}I\left(\boldsymbol{x},\boldsymbol{y}\right)&=-\frac{1}{2}\ln\operatorname*{det}\left(\boldsymbol{1}-\boldsymbol{\Sigma}_{xx}^{-1}\boldsymbol{\Sigma}_{xy}\boldsymbol{\Sigma}_{yy}^{-1}\boldsymbol{\Sigma}_{yx}\right)\\\\&=-\frac{1}{2}\ln\operatorname*{det}\left(\boldsymbol{1}-\boldsymbol{\Sigma}_{yy}^{-1}\boldsymbol{\Sigma}_{yx}\boldsymbol{\Sigma}_{xx}^{-1}\boldsymbol{\Sigma}_{xy}\right)\end{aligned}
